Hard magnet material exploration#
Introduction#
In this notebook we explore hard magnet properties such as Hc as function of material and temperature.
For more in-depth explanations we recommend starting with the hard magnet tutorial.
Requirements:
Software:
mammos,esys-escriptBasic understanding of mammos-units and mammos-entity
[1]:
%config InlineBackend.figure_format = "retina"
import math
import time
import mammos_analysis
import mammos_dft
import mammos_mumag
import mammos_spindynamics
import mammos_units as u
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colormaps
[2]:
# Allow convenient conversions between A/m and T
u.set_enabled_equivalencies(u.magnetic_flux_field());
Select material#
Change the index in the first line of the following cell to select one of the available materials:
[3]:
index = 1 # select desired material
match index:
case 1:
material = "Co2Fe2H4"
H_max = (5 * u.T).to("A/m")
case 2:
material = "Fe16N2"
H_max = (1.2 * u.T).to("A/m")
material
[3]:
'Co2Fe2H4'
Load data from DFT and spindynamics databases#
[4]:
results_dft = mammos_dft.db.get_micromagnetic_properties(material)
[5]:
results_spindynamics = mammos_spindynamics.db.get_spontaneous_magnetization(material)
Calculate micromagnetic intrinsic properties using Kuz’min formula#
[6]:
results_kuzmin = mammos_analysis.kuzmin_properties(
T=results_spindynamics.T,
Ms=results_spindynamics.Ms,
K1_0=results_dft.Ku_0,
)
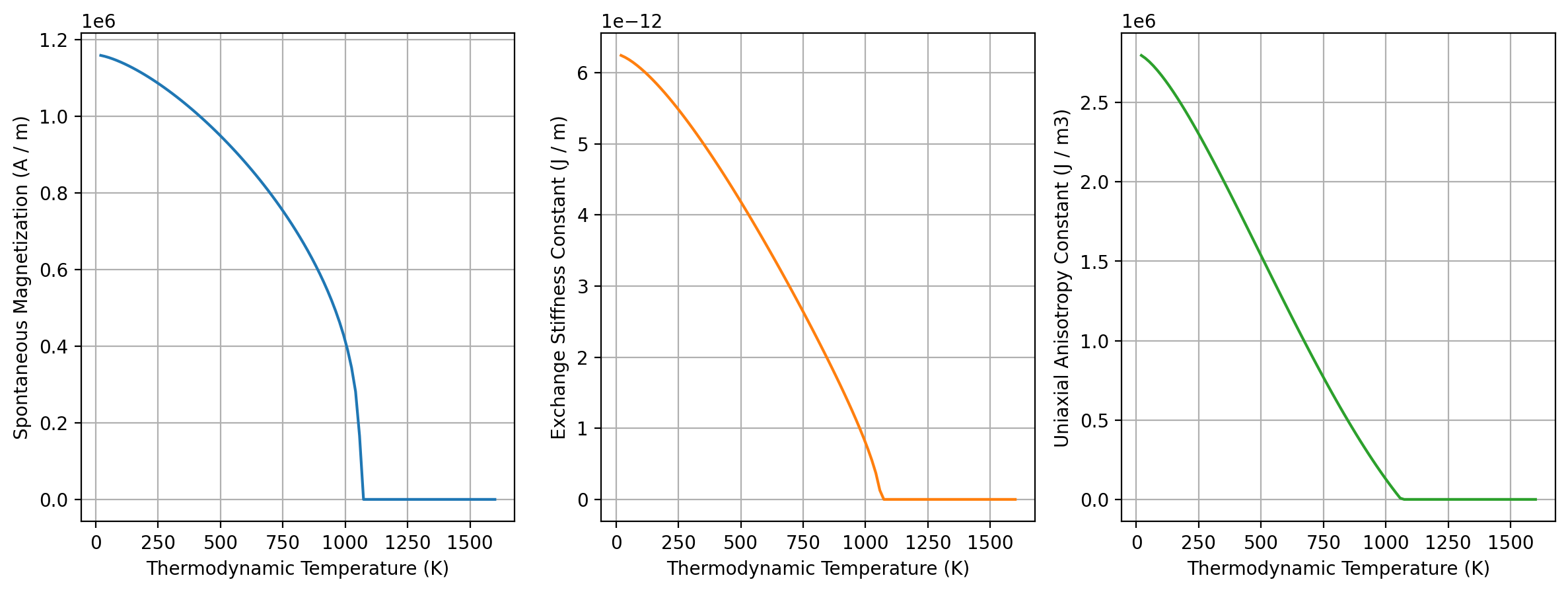
[7]:
results_kuzmin.plot();
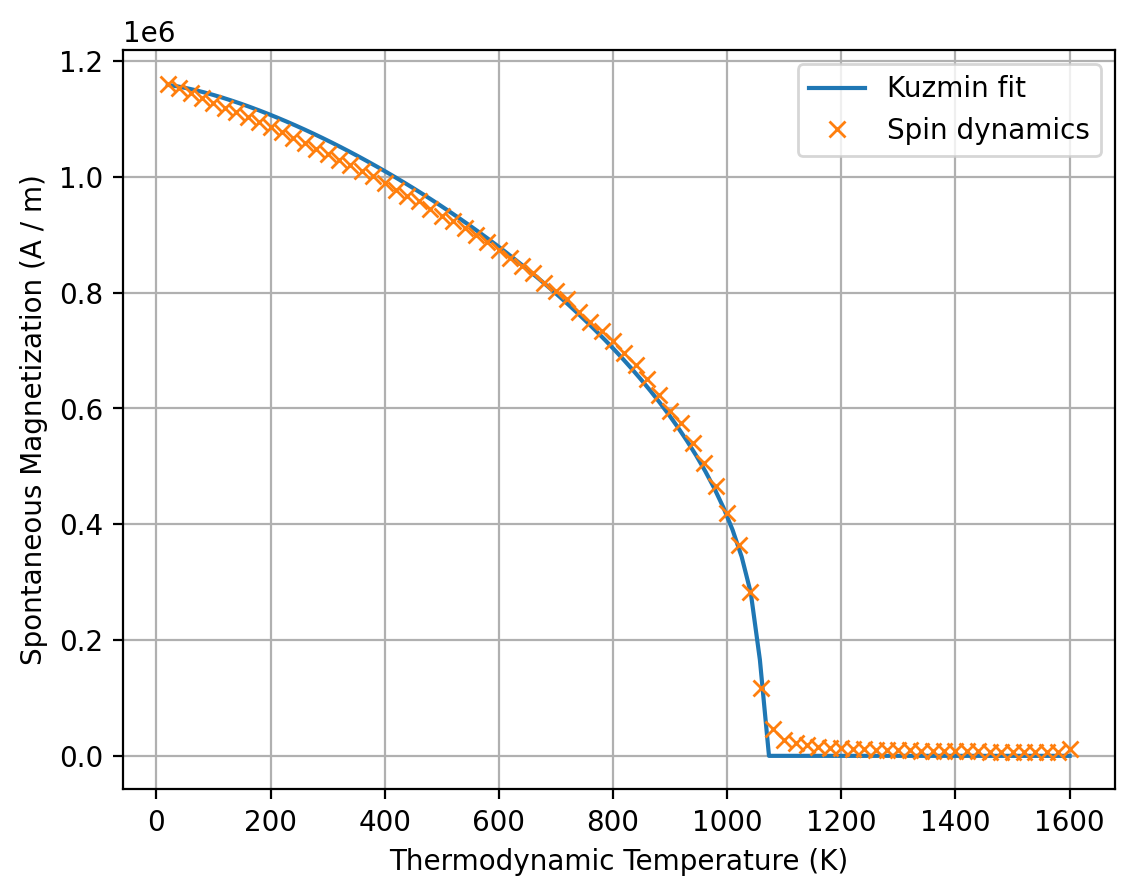
[8]:
ax = results_kuzmin.Ms.plot(label="Kuzmin fit")
results_spindynamics.plot(ax=ax, label="Spin dynamics");
Compute Hc(T)#
[9]:
T = np.linspace(0, 1.1 * results_kuzmin.Tc.q, 7)
simulations = []
start_time = time.time()
for temperature in T:
print(f"Running simulation for T={temperature:.0f}, {int(time.time() - start_time)} seconds")
results_hysteresis = mammos_mumag.hysteresis.run(
mesh="cube20_singlegrain_msize2",
Ms=results_kuzmin.Ms(temperature),
A=results_kuzmin.A(temperature),
K1=results_kuzmin.K1(temperature),
theta=0,
phi=0,
h_start=H_max,
h_final=-H_max,
h_n_steps=30,
)
simulations.append(results_hysteresis)
Running simulation for T=0 K, 0 seconds
Running simulation for T=195 K, 25 seconds
Running simulation for T=389 K, 47 seconds
Running simulation for T=584 K, 69 seconds
Running simulation for T=778 K, 92 seconds
Running simulation for T=973 K, 115 seconds
Running simulation for T=1168 K, 138 seconds
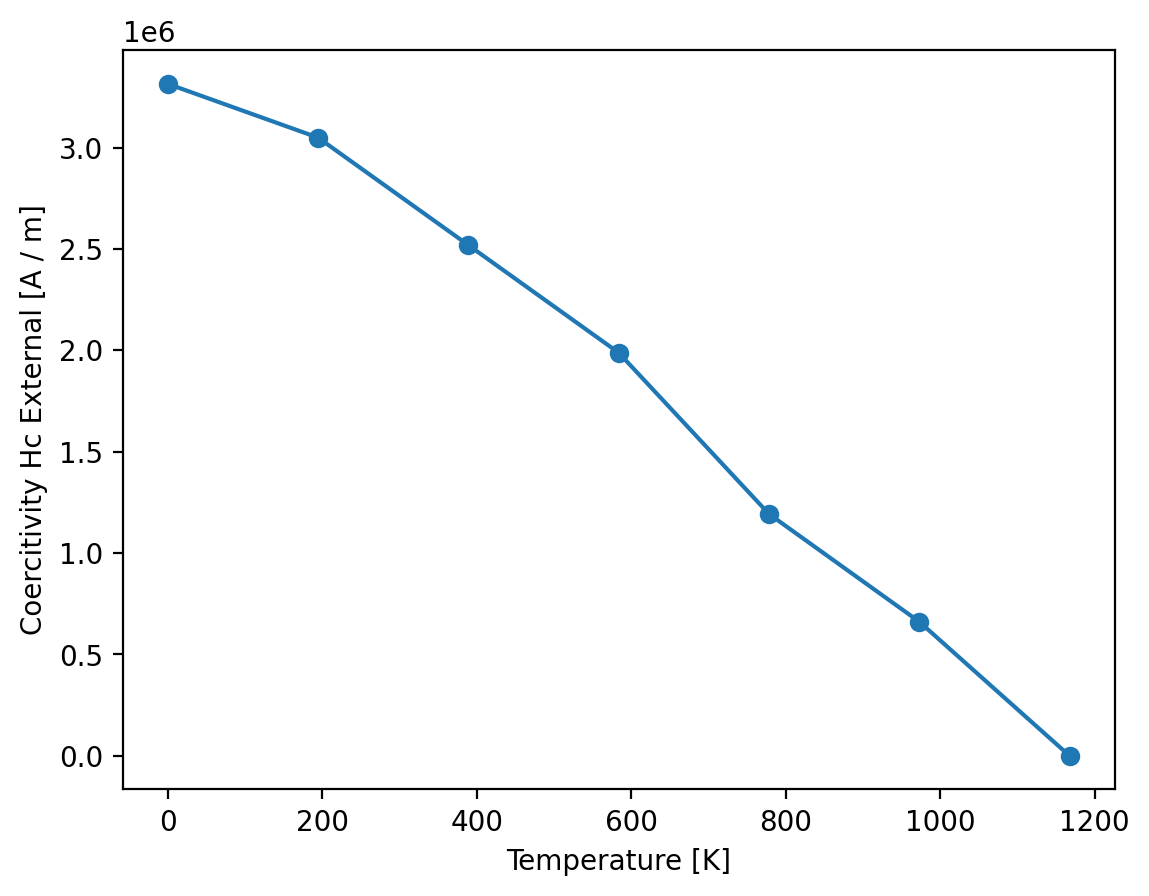
We can now use mammos_analysis.hysteresis as shown before to extract Hc for all simulations and visualize Hc(T):
[10]:
Hcs = []
for res in simulations:
cf = mammos_analysis.hysteresis.extract_coercive_field(H=res.H, M=res.M).value
if np.isnan(cf): # Above Tc
cf = 0
Hcs.append(cf)
[11]:
plt.plot(T, Hcs, linestyle="-", marker="o")
plt.xlabel("Temperature [K]")
plt.ylabel("Coercitivity Hc External [A / m]");
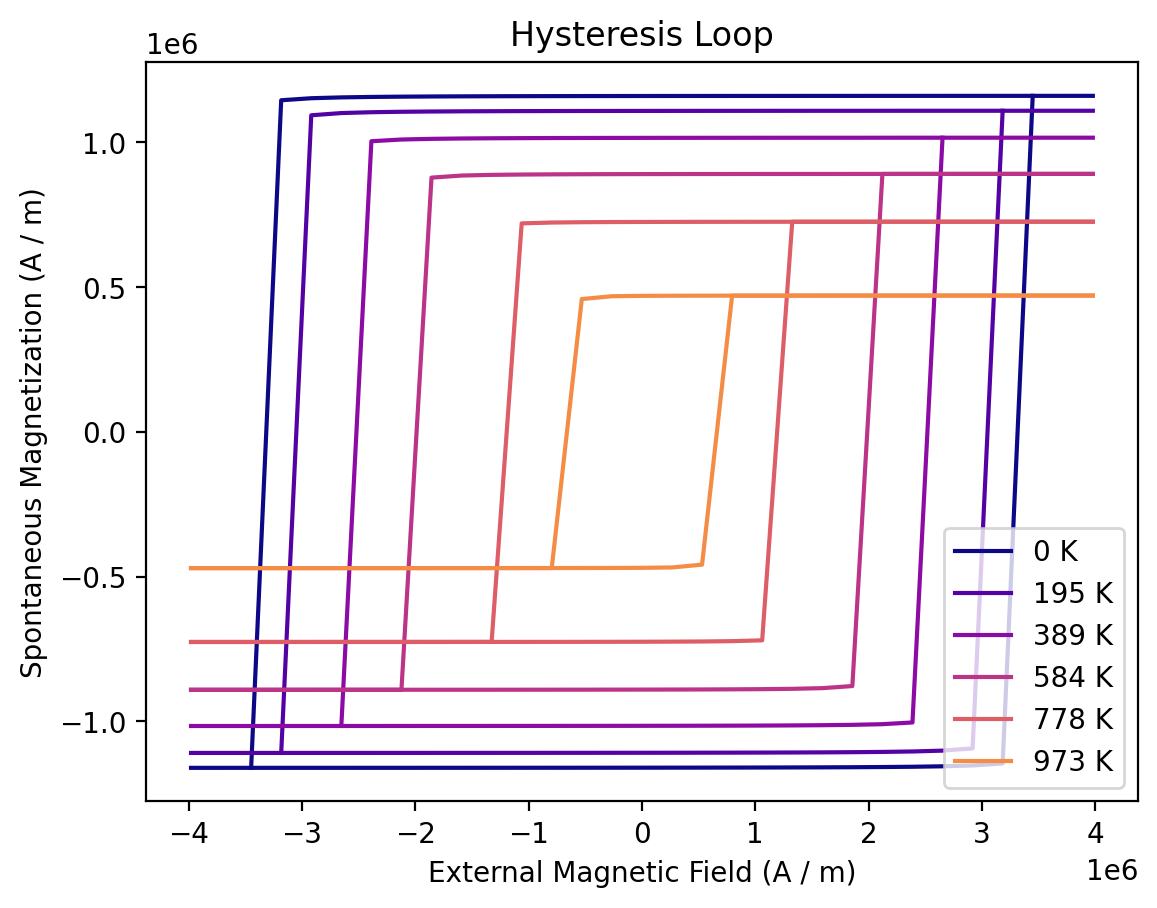
We can also show the hysteresis loops of all simulations:
[12]:
colors = colormaps["plasma"].colors[:: math.ceil(256 / len(T))]
fix, ax = plt.subplots()
for temperature, sim, color in zip(T, simulations, colors, strict=False):
if np.isnan(sim.M.q).all(): # no Ms above Tc
continue
sim.plot(ax=ax, label=f"{temperature:.0f}", color=color, duplicate_change_color=False)
ax.legend(loc="lower right");