mammos_mumag quickstart#

mammos_mumag can compute hysteresis loops of magnetic materials using finite elements.

Requirements:

  • mammos and esys-escript

[1]:

import mammos_entity as me
import mammos_units as u
import pandas as pd
from mammos_mumag import hysteresis

[2]:

u.set_enabled_equivalencies(u.magnetic_flux_field())

[2]:

<astropy.units.core._UnitContext at 0x7f9b33f16dd0>

Hysteresis simulation#

The hysteresis.run function computes a hysteresis loop for a homogeneous material with given parameters. We need to pass in a suitable mesh, mammos_mumag.mesh provides a sample mesh.

[3]:

hysteresis_result = hysteresis.run(
    mesh="cube20_singlegrain_msize2",
    Ms=me.Ms(1280000, unit="A/m"),
    A=me.A(7.7e-12, unit="J/m"),
    K1=me.Ku(4300000, unit="J/m3"),
    theta=0,
    phi=0,
    h_start=(10 * u.T).to("A/m"),
    h_final=(-10 * u.T).to("A/m"),
    h_n_steps=20,
)

Hysteresis result object#

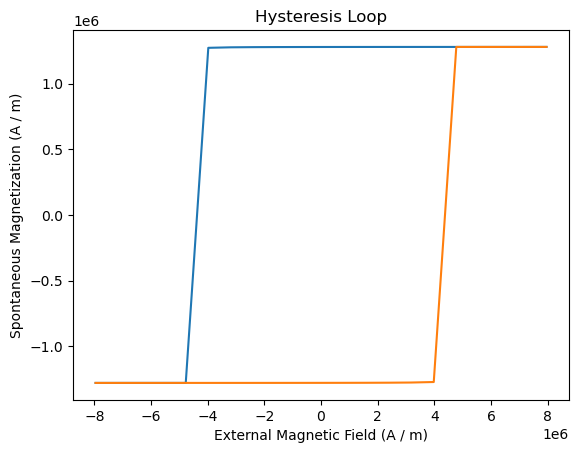
The returned results_hysteresis object provides a plot method to visualize the computed data. mammos_mumag.hysteresis only computes half a hysteresis loop, going from hstart to hfinal. To show a full loop this function mirrors the computed data and plots it twice:

[4]:

hysteresis_result.plot();
../../_images/examples_mammos-mumag_quickstart_6_0.png

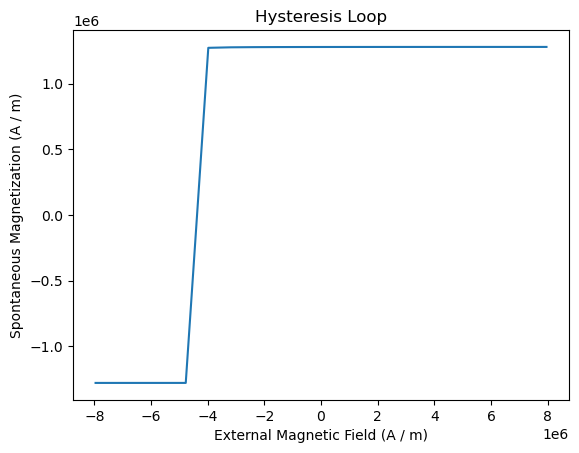
To only see the actual simulation, we can use the flag duplicate=False:

[5]:

hysteresis_result.plot(duplicate=False);
../../_images/examples_mammos-mumag_quickstart_8_0.png

The results object provides access to:

  • the external field H

  • the magnetization M in the direction of the applied field

  • the component Mx, My, Mz of the spontaneous magnetization

  • the energy density

[6]:

hysteresis_result.H

[6]:
ExternalMagneticField(value=
[ 7957747.15026276  7161972.43523649  6366197.72021021  5570423.00518393
  4774648.29015766  3978873.57513138  3183098.86010511  2387324.14507883
  1591549.43005255   795774.71502628        0.          -795774.71502628
 -1591549.43005255 -2387324.14507883 -3183098.86010511 -3978873.57513138
 -4774648.29015766 -5570423.00518393 -6366197.72021021 -7161972.43523649
 -7957747.15026276],
 unit=A / m)
[7]:

hysteresis_result.M

[7]:
SpontaneousMagnetization(value=
[ 1279889.28858392  1279875.35487467  1279858.60865277  1279838.23693916
  1279813.10960708  1279781.61816143  1279741.40923658  1279688.9282623
  1279618.59692456  1279521.24777537  1279380.92895796  1279167.79124963
  1278820.31896709  1278193.40901814  1276865.45558215  1273023.46966246
 -1279813.11387701 -1279838.23510354 -1279858.60560256 -1279875.35242235
 -1279889.28868812],
 unit=A / m)
[8]:

hysteresis_result.Mx

[8]:
SpontaneousMagnetization(value=
[ 1.33369419e+04  1.27642912e+04  1.21138305e+04  1.13685440e+04
  1.05060693e+04  9.49642262e+03  8.29840374e+03  6.85388865e+03
  5.07807497e+03  2.84220258e+03 -5.92135651e+01 -3.97555587e+03
 -9.55402102e+03 -1.81446442e+04 -3.31351859e+04 -6.65045268e+04
 -1.05064987e+04 -1.13683458e+04 -1.21134459e+04 -1.27639874e+04
 -1.33368784e+04],
 unit=A / m)
[9]:

hysteresis_result.My

[9]:
SpontaneousMagnetization(value=
[ -48.88653309  -51.96927457  -55.4673908   -59.47103443  -64.09846682
  -69.5089531   -75.91814415  -83.63248719  -93.09714579 -104.98673227
 -120.37569967 -141.08903498 -170.50557468 -215.70060297 -294.72360668
 -476.0020296    64.14680914   59.35556978   55.25696228   51.80783763
   48.92009087],
 unit=A / m)
[10]:

hysteresis_result.Mz

[10]:
SpontaneousMagnetization(value=
[ 1279851.43397906  1279847.49250133  1279842.09608478  1279834.72859929
  1279824.6500327   1279810.77494583  1279791.46867247  1279764.19052806
  1279724.84138717  1279666.49962956  1279576.79725706  1279431.97819965
  1279181.81279555  1278704.73773844  1277638.20888423  1274378.02605554
 -1279824.64680899 -1279834.73022376 -1279842.09974628 -1279847.4953512
 -1279851.43519197],
 unit=A / m)
[11]:

hysteresis_result.energy_density

[11]:
EnergyDensity(value=
[-16793259.14717998 -15513376.61777121 -14233509.37078527
 -12953660.60369528 -11673834.47507029 -10394036.49593287
  -9114274.12985359  -7834557.74471192  -6554902.1835602
  -5275329.48376666  -3995873.86584996  -2716591.57883736
  -1437582.25793929   -159041.64107598   1118580.91577263
   2393925.95515716 -11673834.47506085 -12953660.60369348
 -14233509.37077219 -15513376.61776414 -16793259.14717655],
 unit=J / m3)

The attribute configuration_type contains a list of indices that refer to saved magnetization field configurations. We will use this information later.

[12]:

hysteresis_result.configuration_type

[12]:

array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2])

We can also get the hysteresis data as a pandas dataframe in SI units:

[13]:

hysteresis_result.dataframe

[13]:
configuration_type H M Mx My Mz energy_density
0 1 7.957747e+06 1.279889e+06 13336.941917 -48.886533 1.279851e+06 -1.679326e+07
1 1 7.161972e+06 1.279875e+06 12764.291238 -51.969275 1.279847e+06 -1.551338e+07
2 1 6.366198e+06 1.279859e+06 12113.830536 -55.467391 1.279842e+06 -1.423351e+07
3 1 5.570423e+06 1.279838e+06 11368.544042 -59.471034 1.279835e+06 -1.295366e+07
4 1 4.774648e+06 1.279813e+06 10506.069334 -64.098467 1.279825e+06 -1.167383e+07
5 1 3.978874e+06 1.279782e+06 9496.422618 -69.508953 1.279811e+06 -1.039404e+07
6 1 3.183099e+06 1.279741e+06 8298.403739 -75.918144 1.279791e+06 -9.114274e+06
7 1 2.387324e+06 1.279689e+06 6853.888646 -83.632487 1.279764e+06 -7.834558e+06
8 1 1.591549e+06 1.279619e+06 5078.074971 -93.097146 1.279725e+06 -6.554902e+06
9 1 7.957747e+05 1.279521e+06 2842.202583 -104.986732 1.279666e+06 -5.275329e+06
10 1 0.000000e+00 1.279381e+06 -59.213565 -120.375700 1.279577e+06 -3.995874e+06
11 1 -7.957747e+05 1.279168e+06 -3975.555866 -141.089035 1.279432e+06 -2.716592e+06
12 1 -1.591549e+06 1.278820e+06 -9554.021016 -170.505575 1.279182e+06 -1.437582e+06
13 1 -2.387324e+06 1.278193e+06 -18144.644173 -215.700603 1.278705e+06 -1.590416e+05
14 1 -3.183099e+06 1.276865e+06 -33135.185913 -294.723607 1.277638e+06 1.118581e+06
15 1 -3.978874e+06 1.273023e+06 -66504.526815 -476.002030 1.274378e+06 2.393926e+06
16 2 -4.774648e+06 -1.279813e+06 -10506.498737 64.146809 -1.279825e+06 -1.167383e+07
17 2 -5.570423e+06 -1.279838e+06 -11368.345772 59.355570 -1.279835e+06 -1.295366e+07
18 2 -6.366198e+06 -1.279859e+06 -12113.445946 55.256962 -1.279842e+06 -1.423351e+07
19 2 -7.161972e+06 -1.279875e+06 -12763.987414 51.807838 -1.279847e+06 -1.551338e+07
20 2 -7.957747e+06 -1.279889e+06 -13336.878392 48.920091 -1.279851e+06 -1.679326e+07

We can generate a table in alternate units:

[14]:

df = pd.DataFrame(
    {
        "mu0_H": hysteresis_result.H.q.to(u.T),
        "J": hysteresis_result.M.q.to(u.T),
    },
)
df.head()

[14]:
mu0_H J
0 10.0 1.608356
1 9.0 1.608339
2 8.0 1.608318
3 7.0 1.608292
4 6.0 1.608261

Visualizing magnetization configurations#

To plot the hysteresis loop (including the available configurations), run

[15]:

hysteresis_result.plot(configuration_marks=True);
../../_images/examples_mammos-mumag_quickstart_23_0.png

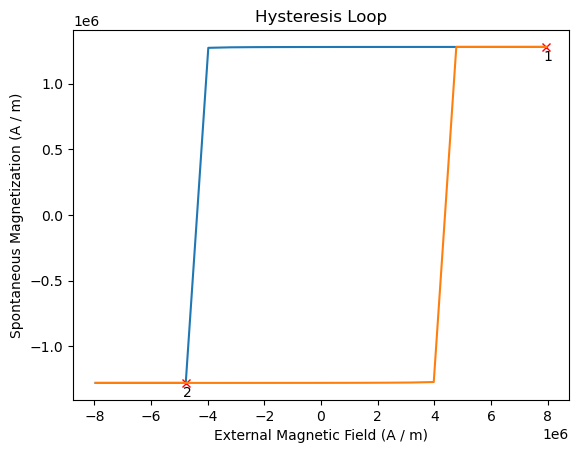
We can get the location of the saved configurations from the attribute configurations:

[16]:

hysteresis_result.configurations

[16]:

{1: PosixPath('/home/petrocch/repo/mammos/mammos-mumag/examples/hystloop/hystloop_0001.vtu'),
 2: PosixPath('/home/petrocch/repo/mammos/mammos-mumag/examples/hystloop/hystloop_0002.vtu')}

To inspect the configurations more conveniently directly in the notebook we can use the plot_configuration function of hysteresis_result. We need to pass the index and get an interactive 3D plot (using pyvista):

[17]:

hysteresis_result.plot_configuration(1)

 JS Error => TypeError: `target` argument of Proxy must be an object, got null

Note: the small object size is a consequence of the empty sphere around the cube.