Design#
We discuss the design of the MaMMoS framework, and the use of ontology labels and units when exchanging data.
TLDR#
The MaMMoS framework is composed of specialized components (typically Python packages) from which complex workflows (typically Python scripts or notebooks) can be created. Figure 1 shows a graphical overview.
The use of ontology labels and units (through
mammos-entity) is supported and encouraged, but not compulsory. A more detailed summary is available at the end of this page at Design principles for ontology labels and units.
MaMMoS framework architecture#
The Magnetic Multiscale Modelling Suite (MaMMoS) provides tools to help researchers and engineers to accelerate the development of designs for future devices.
To make this ambitious aim tractable, we use the following design strategy:
Develop (small) units of functionality (such as Python packages, classes or functions).
The units may depend on each other where needed (to avoid code duplication), but should be as independent from each other as possible.
More complex tasks can be solved by combining the use of multiple units of functionality in a (Python) script or Jupyter Notebook. These are called workflows.
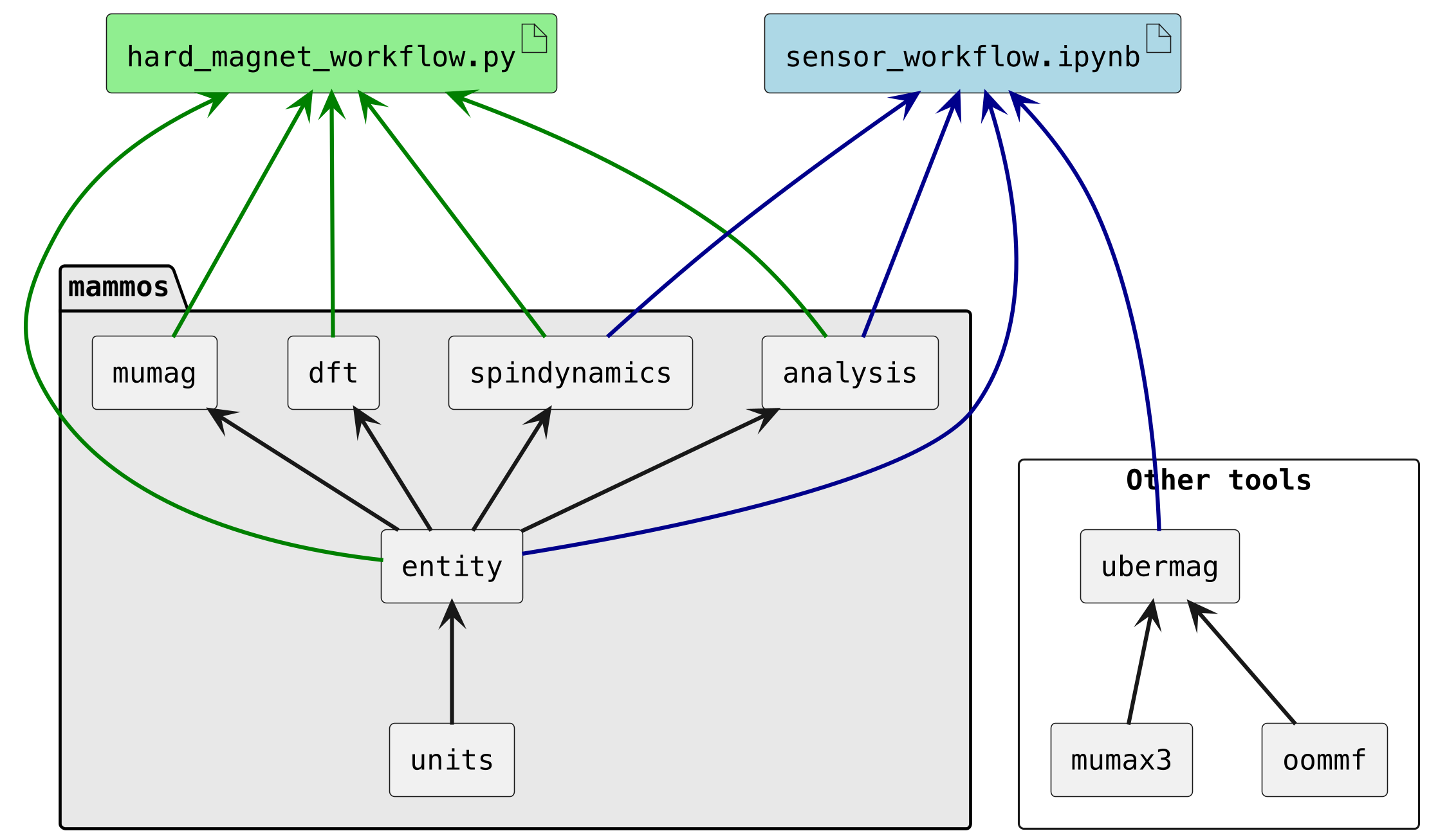
Figure 1 Overview of the components of the MaMMoS software (in box
mammos), their interdependencies, how they can be combined
to form workflows (hard_magnet_workflow and sensor_workflow), and how
existing tools of the research software for magnetism can be connected
(example: ubermag).
Arrows show which package is used by which other package: e.g., the mammos-entity
package uses the mammos-units package (through an import). The
hard_magnetic_workflow.py makes use of the mammos-mumag package.#
Framework components#
Figure 1 shows an overview of the components of
the MaMMoS software, and how specific workflows can be composed out of those.
The MaMMoS framework is a set of libraries that are united by the prefix
mammos and in the figure shown together as the package on the left with the
light gray background. The Python meta package mammos can be used to install
all of the components together. The mammos framework components are:
mammos-unitsproviding Quantity objects (values with units)mammos-entityproviding Entity objects (Quantity and EMMO ontology label)mammos-spindynamicsproviding spindynamics-based magnetic material propertiesmammos-dftproviding DFT-based magnetic material propertiesmammos-mumagproviding finite-element micromagnetic hysteresis simulationsmammos-analysisproviding post-processing tools (hysteresis loop, kuzmin, …)
Workflows#
Out of these components, complete workflows can be constructed, that help with particular magnetic material research or design questions. Within MaMMoS, a Python program or a (Python) Jupyter Notebook can be used to execute a sequence of operations making use of the MaMMoS framework components (and other already existing tools if desired).
The figures shows two demonstrator workflows:
Hard magnet workflow shown in green in Figure 1 (see hard magnetic workflow tutorial).
Sensor workflow shown in blue in Figure 1 (see sensor workflow example).
Through choosing Python as the environment within which the MaMMoS capabilities are (most easily) accessible, users can immediately connect all existing magnetic research tools that have a Python interface (such us Ubermag in the sensor workflow example).
As the workflows are defined through a Python program, there is (great) freedom to define new workflows to address requirements that may not be known at the moment: We strive to make the MaMMoS components as powerful, flexible and robust as possible within the scope of the MaMMoS project, and use them in workflows that are of interest to project partners. The biggest potential impact of the project is in the future use of the MaMMoS components and tools (individually or together) for new tasks and workflows, that may not even be known yet.
FAIR data and ontologies#
FAIR data#
In the context of open science, it is essential that numerical values in data are consistently associated both units and ontology labels.
We use the term quantity to refer to a value (such as a number, vector or array) with associated units. (mammos-units)
We understand entity as a value with associated units that has a label from an ontology, such as the EMMO. (mammos-entity)
Units ensure that values are comparable across datasets, avoiding ambiguity about scale or dimension. Entities—through they ontology-based labels—provide precise semantic definitions for the quantities being measured, ensuring clarity about what numbers actually represent, and making measurements interpretable.
Example: we measure spontaneous magnetization in units of ampere per meter, and imagine that \(M_\mathrm{s} = 10^5 \mathrm{A/m}\). If we wanted to be absolutely clear what we talk about, we could refer to our entity as a triplet:
(SpontaneousMagnetization, 1e5, A/m)
Together, Ontology labels, values and units make data more Findable, Accessible, Interoperable, and Reusable (FAIR) by enabling machines and researchers alike to interpret and integrate data correctly across disciplines and domains.
Ontology labels (mammos-entity)#
We have created the mammos-entity package to support the use of units and ontology labels in day-to-day data-focused research.
To define an entity for \(M_\mathrm{s}\) as in the example above, we could write:
Ms = mammos_entity.Entity("SpontaneousMagnetisation", 1e5, "A/m")
Here SpontaneousMagnetization links back to the SpontaneousMagnetization EMMO
ontology entry.
As this entity is often needed in magnetic research, there is an abbreviation available:
Ms = mammos_entity.Ms(1e5, "A/m")
The object Ms knows its ontology label (SpontaneousMagnetization), and
the value (1e5) and the units (A/m) of the value. When this is passed to
other functions, they can check that the entity is of the right type for the
analysis to make sense, and what the units are so that the value makes sense
(for example: do we measure in ampere per meter or in kilo ampere per meter).
The example above uses a single float as the value but entities do similar support vectors or any array-like data structure.
An entity object behaves very much like a float or a numpy array. If needed, one
can get to the numerical value (here 1e5) through the attribute
Ms.value.
Use of ontology-labels: supported, desired or enforced?#
The use of entities makes data exchange more robust, self-documenting, and machine readable. The use of entities (and thus units) reduces the number of implicit assumptions that can lead to errors or non-re-usable data. In the spirit of fairer data, using entities is highly desirable.
However, there are at least two practical aspects to consider:
If a researcher needs to express all their data in entities, they have to type more than if they were just using a floating point number. For example,
mammos_entity.Ms(1e5, "A/m")instead of1e5. While we would argue that the increased clarity and improved readability is more important than the one-off effort of writing this, some may object.If the researcher works with entities and needs to make use of a third-party function that expects a floating point number (perhaps a tool from
scipy, or—as a illustrative example—math.cos()), then it is possible that the entity cannot be used. Instead ofmath.cos(Ms)one would need to writemath.cos(Ms.value)whereMs.valuegives access to just the value of the entity (1e5in our example).
Aspect 1 requires a bit more verbosity in writing the code (including clarity in the process), aspect 2 needs translation of the entity to other tools which—at that very point–increases complexity of the code.
There is thus a trade-off: in principle, the use of entities is desirable. However, there is a cost for doing so. To convince researchers to embrace ontologies (for example through using entities), we need to reduce the practical burden as much as possible.
Example#
First we describe a use case as a concrete example, followed by three different options of passing data to this. Based on this, we then summarise our approach towards encouragement of use of entities.
Imagine a function of the MaMMoS software that returns the exchange coupling constant as a
function of temperature. We assuming the function is called f and takes a
temperature T, and we want to evaluate it at a temperature of 100 Kelvin.
Here are three options how we could pass the temperature (entity) to the function:
Option 1: just the value#
>>> f(100)
The least effort.
Missing information: - units (Kelvin or Celsius or something else)? - What is the semantic meaning (=ontology label)?
Option 2: number and units (=quantity)#
We should say what we mean with 100: if we talk about temperature, it could
be 100 Kelvin or 100 degree Celsius for example. Using
mammos_units, we can be precise:
>>> import mammos_units as u
>>> f(100 * u.Kelvin)
The function f can now check the units of the argument, and complain if
Kelvin is not what was expected.
Missing information: - What is the semantic meaning (=ontology label)?
Option 3: number, units and ontology label (=entity)#
We can also provide the ontology label for the temperature: this provides a more precise semantic definition of the argument, and also avoids misunderstandings (using k:sub: B T one could express energy in units of temperature T, but that’s not what we mean here).
To be as precise as possible, we need to use the ontology label. Using
mammos_entity, we can write
>>> import mammos_entity as me
>>> f(me.Entity("ThermodynamicTemperature", 100, "K"))
or, as an equivalent abbreviation for this:
>>> f(me.T(100, "K"))
With the ontology label, the function f can now check if that is the
expected entity ThermodynamicTemperature and complain if this is not the case.
Discussion#
Option 3 is the best in terms of precision and clarity, and the best for
interoperability and re-usability of data and software. However, it does require
some additional effort to specify the units and the type of the object, in this
example ThermodynamicTemperature.
Once a scientist has used the function f a few times, they may feel very
confident that the input argument meant to be the thermodynamic temperature, and
that of course the function expects input in SI units (i.e. Kelvin). Given that
knowledge, the scientist may prefer option 1.
We argue that a syntax like option 1 is useful to support as for some scientists it would be a game changer (and stop them from using the MaMMoS software) if that functionality was not available.
Design principles for ontology labels and units#
To balance the benefits of a complete specification (option 3) with the convenience of being able to just use a number (option 1), we have developed the following principles within the MaMMoS framework packages:
Return values of functions (and objects behaving like functions):
the principle return values are entities
entities provide as much context as possible and are the FAIRest we can offer
the effort of the scientist to extract just the value (if needed) is small (
.value)
occasionally, there may be additional convenience objects, such as a pandas DataFrame for tabular data in mammos_spindynamics.db.get_spontaneous_magnetization. The DataFrame is a well established object and of great power for data analysis, but cannot carry units.
The convention in this case is that the data is expressed in units of the ontology (such as ampere per meter, or Kelvin, and not in kilo ampere per m or Celsius).
Arguments for functions (and objects behaving like functions) are accepted in the following three options:
Option 1: functions accept (floating point) numbers as input arguments. The assumption is that these are provided in the appropriate SI base units. (Convenient but error prone.)
Option 2: functions accept quantities (i.e. value and unit) as input arguments. There are checked for the correctness of units (prefactors are allowed).
Option 3: functions accept entities (i.e. ontology label, value and unit) as input arguments. These are checked for correctness of the ontology label, and correctness of the units (prefactors are allowed).
This is the best and recommended approach.
Users of the packages can mix the three approaches as they see fit. While consistent use of option 3 would be desirable and is recommded, we have seen in the past that a lack of flexibility can hinder uptake of well-intended improvements.
