Hard magnet tutorial#
Introduction#
In this notebook we explore hard magnet properties such as Hc as function of temperature for Fe16N2.
We query databases to get temperature-dependent inputs for micromagnetic simulations from DFT and spin dynamics simulations
We run hysteresis simulations and compute derived quantities.
Requirements:
Software:
mammos,esys-escriptBasic understanding of mammos-units and mammos-entity
The MODA diagram is provided at the bottom of the notebook.
%config InlineBackend.figure_format = "retina"
import math
import mammos_analysis
import mammos_dft
import mammos_entity as me
import mammos_mumag
import mammos_spindynamics
import mammos_units as u
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from matplotlib import colormaps
# Allow convenient conversions between A/m and T
u.set_enabled_equivalencies(u.magnetic_flux_field());
DFT data: magnetization and anisotropy at zero Kelvin#
The first step loads spontaneous magnetization Ms_0 and the uniaxial anisotropy constant K1_0 from a database of DFT calculations (at T=0K).
We can use the print_info flag to trigger printing of crystallographic information.
material = "Fe2.33Ta0.67Y"
results_dft = mammos_dft.db.get_micromagnetic_properties(material, print_info=True)
Found material in database.
Chemical Formula: Fe2.33Ta0.67Y Space group name: Space group number: 0 Cell length a: 5.227483 Angstrom Cell length b: 5.227483 Angstrom Cell length c: 25.022642 Angstrom Cell angle alpha: 90.0 deg Cell angle beta: 90.0 deg Cell angle gamma: 120.0 deg Cell volume: 592.173679 Angstrom3 ICSD_label: OQMD_label:
results_dft
MicromagneticProperties(Ms_0=Entity(ontology_label='SpontaneousMagnetization', value=612746.0, unit='A / m'), Ku_0=Entity(ontology_label='UniaxialAnisotropyConstant', value=2170000.0, unit='J / m3'))
results_dft.Ms_0
results_dft.Ku_0
Temperature-dependent magnetization data from spindynamics database lookup#
In the second step we use a spin dynamics calculation database to load data for the temperature-dependent magnetization.
results_spindynamics = mammos_spindynamics.db.get_spontaneous_magnetization(material)
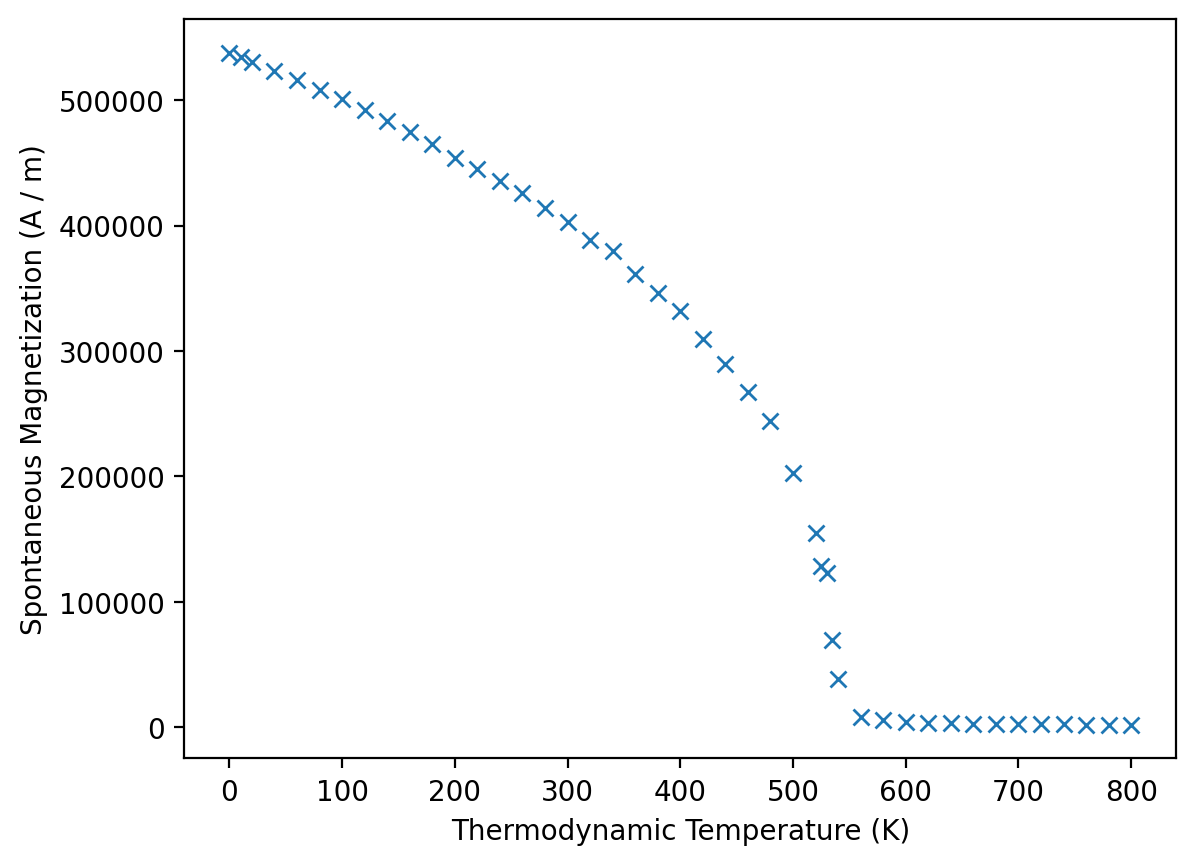
We can visualize the pre-computed data using .plot.
results_spindynamics.plot();
We can access T and Ms and get mammos_entity.Entity objects:
results_spindynamics.T
[ 0. 10. 20. 40. 60. 80. 100. 120. 140. 160. 180. 200. 220. 240.
260. 280. 300. 320. 340. 360. 380. 400. 420. 440. 460. 480. 500. 520.
525. 530. 535. 540. 560. 580. 600. 620. 640. 660. 680. 700. 720. 740.
760. 780. 800.],
unit=K)
results_spindynamics.Ms
[537694.07444336 534210.10153311 530764.36752639 523250.14178896
515738.21821309 508258.87022332 500540.39671216 492131.18264609
483755.61631564 474766.62259313 465115.79688732 454004.77916792
445207.47657222 435913.90029753 425917.95755204 414302.25010872
402869.23234052 388787.20606118 379379.38008579 361089.6076117
346183.4601142 331512.12322956 309325.38617621 289791.026683
267567.34750083 244087.28601035 203117.830414 154867.46065703
128531.95780149 123413.79484906 69795.21779487 38606.54426671
8527.81909467 5671.83537323 4545.6331974 3692.62583725
3234.4405333 2939.70207986 2710.10548472 2571.55219002
2332.28679587 2289.83246349 2162.04656916 2067.34541027
2000.64899435],
unit=A / m)
We can get also the data in the form of a pandas.DataFrame, which only contains the values in SI units:
results_spindynamics.dataframe.head()
| T | Ms | |
|---|---|---|
| 0 | 0.0 | 537694.074443 |
| 1 | 10.0 | 534210.101533 |
| 2 | 20.0 | 530764.367526 |
| 3 | 40.0 | 523250.141789 |
| 4 | 60.0 | 515738.218213 |
Calculate micromagnetic intrinsic properties using Kuz’min formula#
We use Kuz’min equations to compute Ms(T), A(T), K1(T)
Kuz’min, M.D., Skokov, K.P., Diop, L.B. et al. Exchange stiffness of ferromagnets. Eur. Phys. J. Plus 135, 301 (2020). https://doi.org/10.1140/epjp/s13360-020-00294-y
Additional details about inputs and outputs are available in the API reference
results_kuzmin = mammos_analysis.kuzmin_properties(
T=results_spindynamics.T,
Ms=results_spindynamics.Ms,
K1_0=results_dft.Ku_0,
)
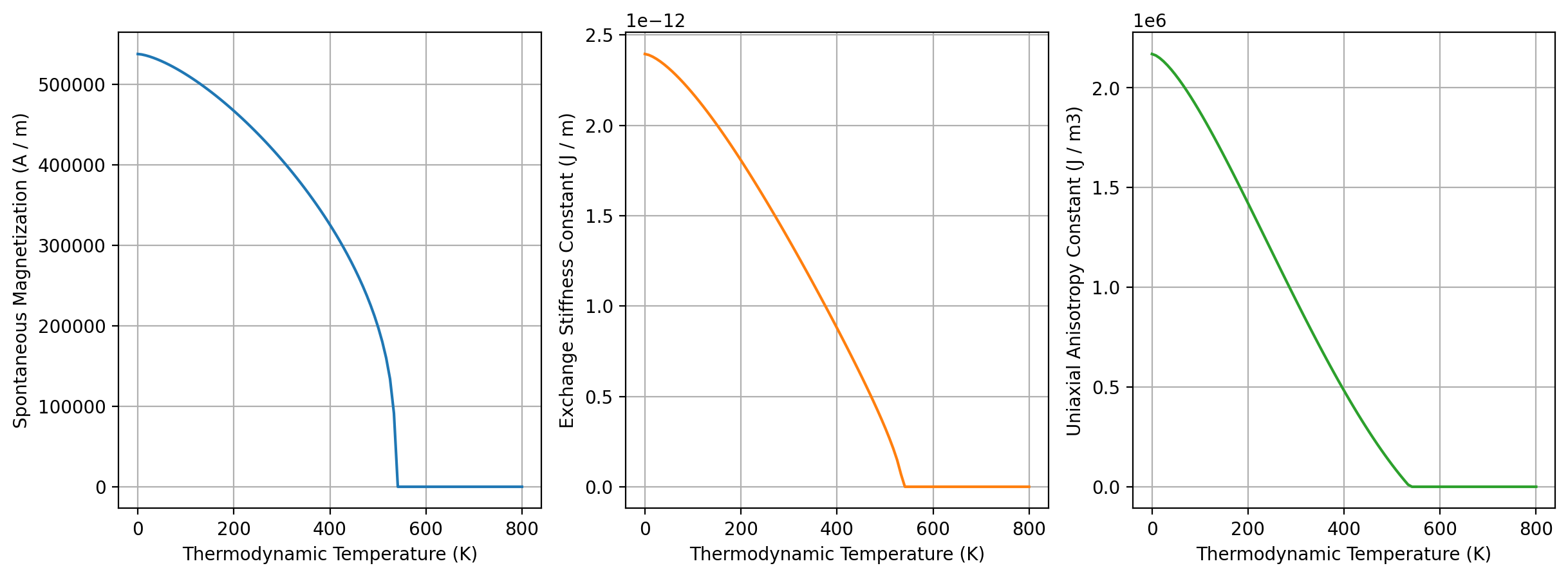
The plot method of the returned object can be used to visualize temperature-dependence of all three quantities. The temperature range matches that of the fit data:
results_kuzmin.plot();
results_kuzmin
KuzminResult(Ms=Ms(T), A=A(T), Tc=Entity(ontology_label='CurieTemperature', value=537.188901303706, unit='K'), s=<Quantity 1.82478202>, K1=K1(T))
The attributes
Ms,AandK1provide fit results as function of temperature. They each have aplotmethod.Tcis the fitted Curie temperature.sis a fit parameter in the Kuzmin equation.
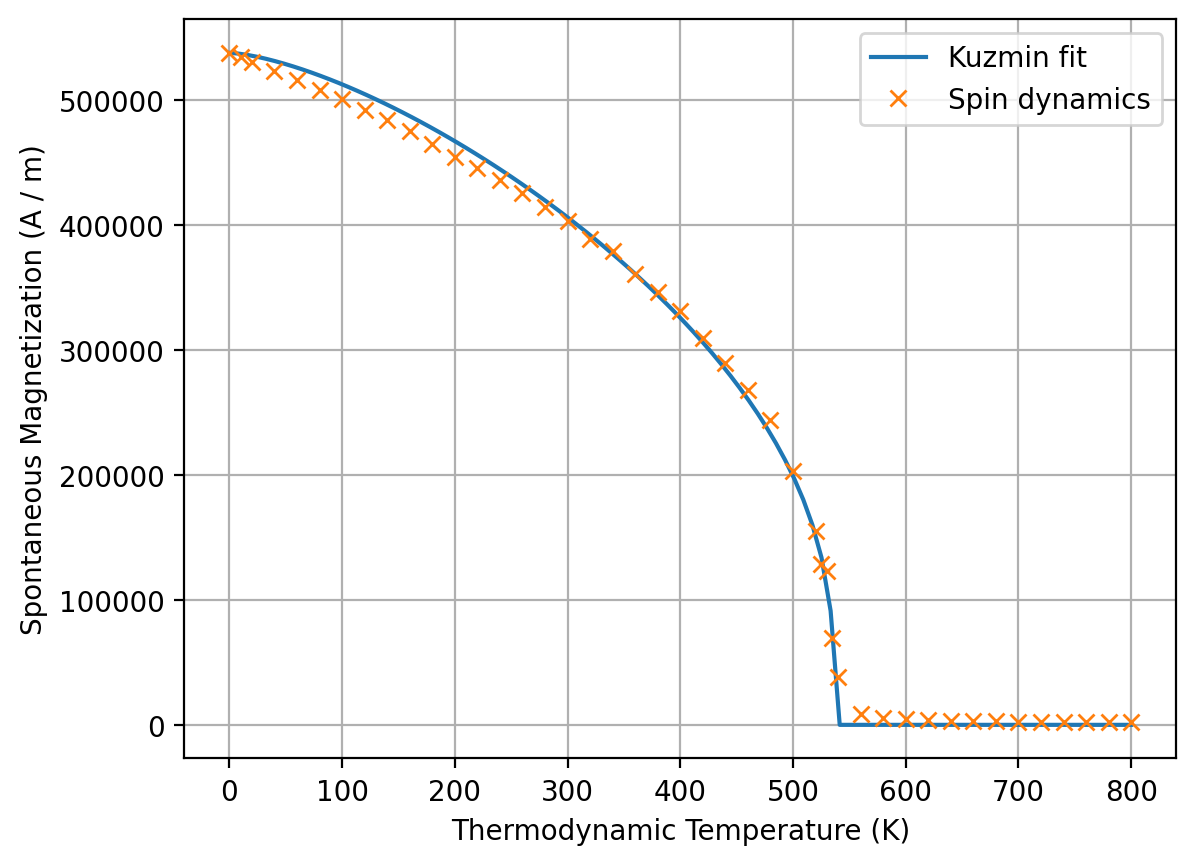
To visually assess the accuracy of the fit, we can combine the plot methods of results_kuzmin.Ms and results_spindynamics:
ax = results_kuzmin.Ms.plot(label="Kuzmin fit")
results_spindynamics.plot(ax=ax, label="Spin dynamics");
To get inputs for the micromagnetic simulation at a specific temperature we call the three attributes Ms, A and K1. We can pass a mammos_entity.Entity, an astropy.units.Quantity or a number:
temperature = me.T(300)
temperature
results_kuzmin.Ms(temperature) # Evaluation with Entity
results_kuzmin.A(300 * u.K) # Evaluation with Quantity
results_kuzmin.K1(300) # Evaluation with number
Run micromagnetic simulation to compute hysteresis loop#
We now compute a hysteresis loop (using a finite-element micromagnetic simulation) with the material parameters we have obtained.
We simulate a 20x20x20 nm cube for which a pre-defined mesh is available.
Additional documentation of this step is available this notebook.
results_hysteresis = mammos_mumag.hysteresis.run(
mesh="cube20_singlegrain_msize2",
Ms=results_kuzmin.Ms(temperature),
A=results_kuzmin.A(temperature),
K1=results_kuzmin.K1(temperature),
theta=0,
phi=0,
h_start=(5 * u.T).to(u.A / u.m),
h_final=(-5 * u.T).to(u.A / u.m),
h_n_steps=30,
)
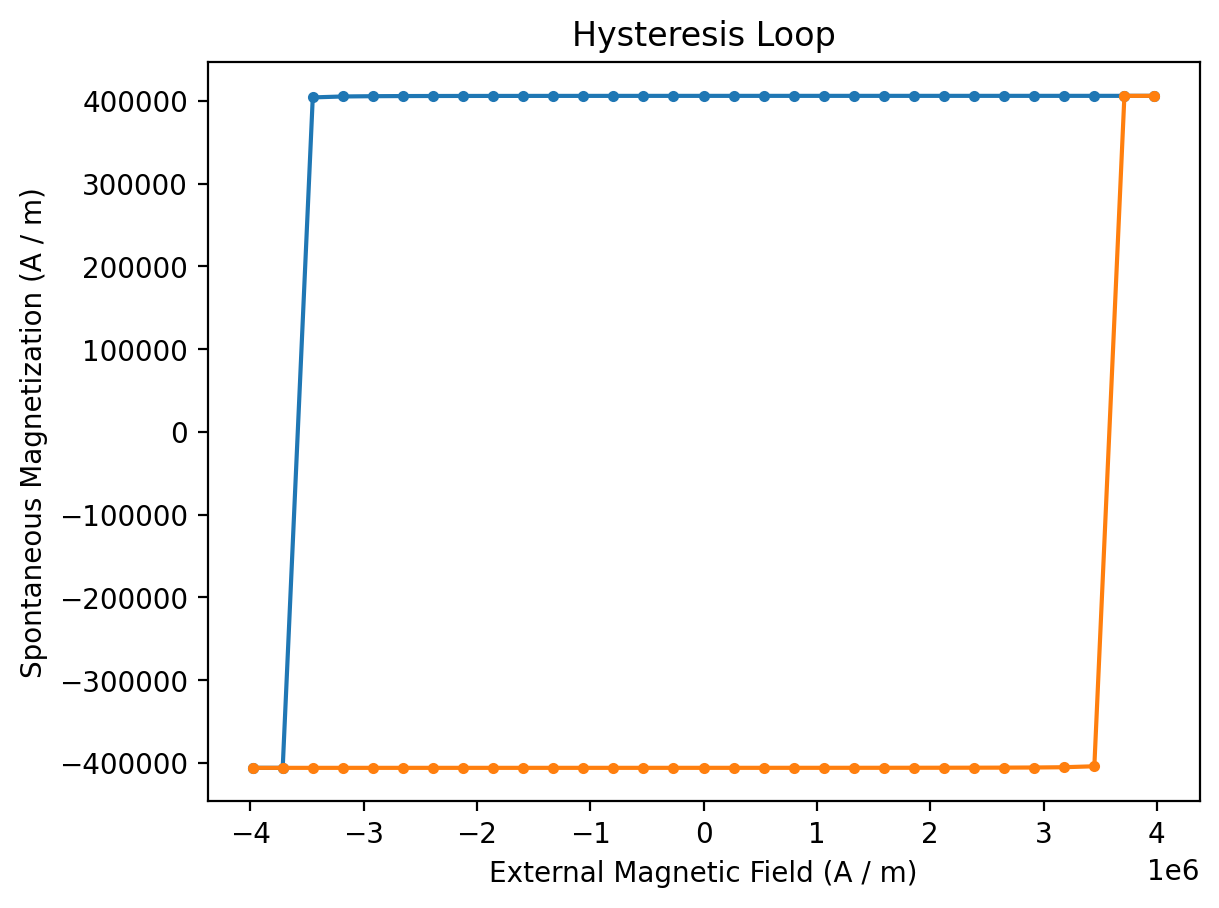
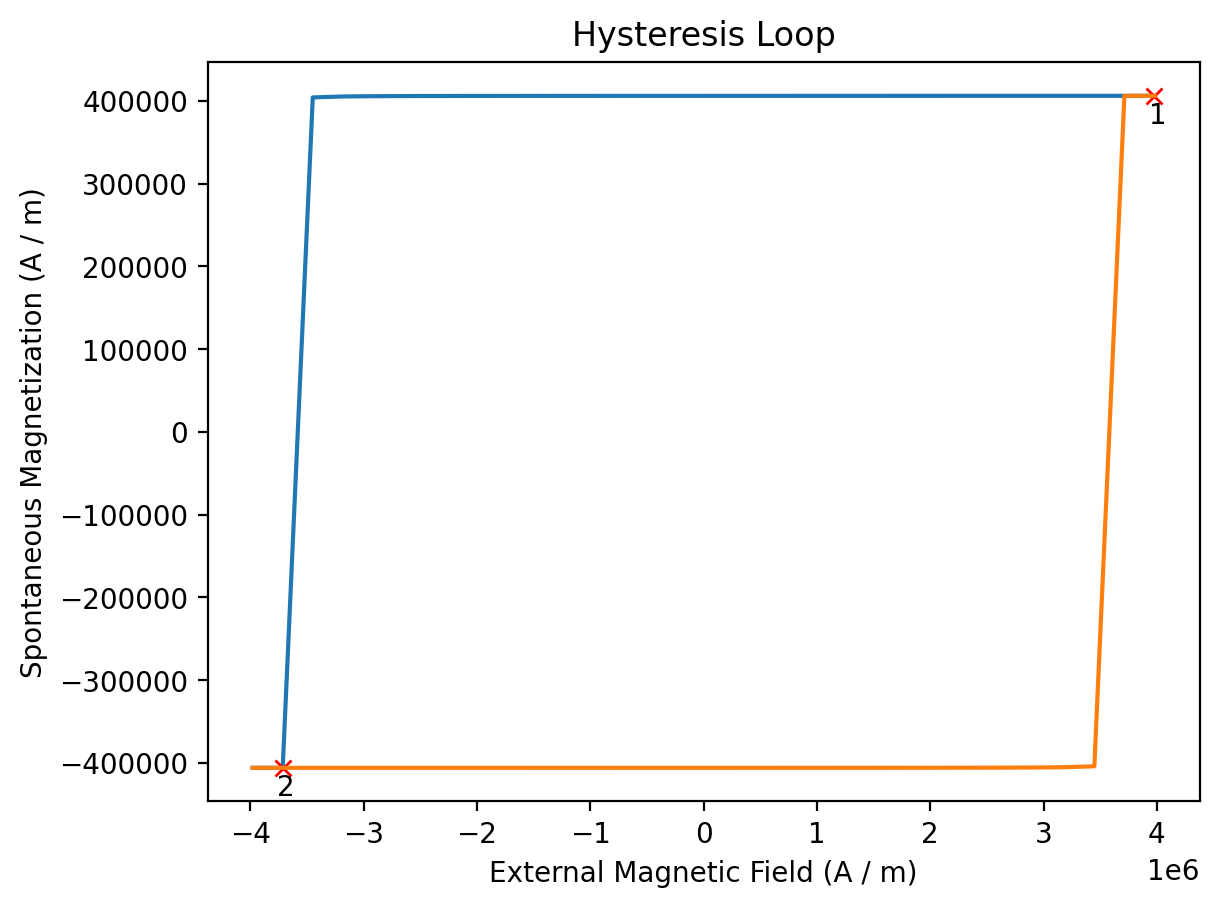
The returned results_hysteresis object provides a plot method to visualize the computed data. mammos_mumag.hysteresis only computes half a hysteresis loop, going from h_start to h_final. To show a full loop this function mirrors the computed data and plots it twice:
results_hysteresis.plot(marker="."); # blue: simulation output, orange: mirrored data
The result object provides access to H and M:
results_hysteresis.H
[ 3.97887358e+06 3.71361534e+06 3.44835710e+06 3.18309886e+06
2.91784062e+06 2.65258238e+06 2.38732415e+06 2.12206591e+06
1.85680767e+06 1.59154943e+06 1.32629119e+06 1.06103295e+06
7.95774715e+05 5.30516477e+05 2.65258238e+05 2.65046223e-10
-2.65258238e+05 -5.30516477e+05 -7.95774715e+05 -1.06103295e+06
-1.32629119e+06 -1.59154943e+06 -1.85680767e+06 -2.12206591e+06
-2.38732415e+06 -2.65258238e+06 -2.91784062e+06 -3.18309886e+06
-3.44835710e+06 -3.71361534e+06 -3.97887358e+06],
unit=A / m)
results_hysteresis.M
[ 406047.44159745 406046.90426802 406046.30879904 406045.6464817
406044.90690923 406044.07755453 406043.14326475 406042.08550617
406040.88148894 406039.50289286 406037.91417839 406036.07025859
406033.91328961 406031.36796102 406028.33484782 406024.68045796
406020.22216639 406014.70476192 406007.76271805 405998.85744887
405987.16834325 405971.39428075 405949.36964165 405917.26558925
405867.76807885 405785.37766127 405632.01099909 405289.1639208
404149.86394112 -406046.90415708 -406047.4416274 ],
unit=A / m)
The dataframe property generates a dataframe in the SI units.
results_hysteresis.dataframe.head()
| configuration_type | H | M | Mx | My | Mz | energy_density | |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 3.978874e+06 | 406047.441597 | -4.121685 | -8.621428 | 406047.441597 | -2.933988e+06 |
| 1 | 1 | 3.713615e+06 | 406046.904268 | -4.270307 | -8.929829 | 406046.904268 | -2.798639e+06 |
| 2 | 1 | 3.448357e+06 | 406046.308799 | -4.430019 | -9.260932 | 406046.308799 | -2.663290e+06 |
| 3 | 1 | 3.183099e+06 | 406045.646482 | -4.602162 | -9.617559 | 406045.646482 | -2.527941e+06 |
| 4 | 1 | 2.917841e+06 | 406044.906909 | -4.788244 | -10.002778 | 406044.906909 | -2.392593e+06 |
We can generate a table in alternate units:
df = pd.DataFrame(
{
"mu0_H": results_hysteresis.H.q.to(u.T),
"J": results_hysteresis.M.q.to(u.T),
},
)
df.head()
| mu0_H | J | |
|---|---|---|
| 0 | 5.000000 | 0.510254 |
| 1 | 4.666667 | 0.510254 |
| 2 | 4.333333 | 0.510253 |
| 3 | 4.000000 | 0.510252 |
| 4 | 3.666667 | 0.510251 |
Plotting of magnetization configurations#
Simulation stores specific magnetization field configurations:
results_hysteresis.plot(configuration_marks=True);
results_hysteresis.configurations
{1: PosixPath('/home/petrocch/repo/mammos/mammos/examples/hystloop/hystloop_0001.vtu'),
2: PosixPath('/home/petrocch/repo/mammos/mammos/examples/hystloop/hystloop_0002.vtu')}
# results_hysteresis.plot_configuration(1);
Analyze hysteresis loop#
We can extract extrinsic properties with the extrinsic_properties function from the mammos_analysis package:
extrinsic_properties = mammos_analysis.hysteresis.extrinsic_properties(
results_hysteresis.H,
results_hysteresis.M,
demagnetization_coefficient=1 / 3,
)
extrinsic_properties.Hc
extrinsic_properties.Mr
extrinsic_properties.BHmax
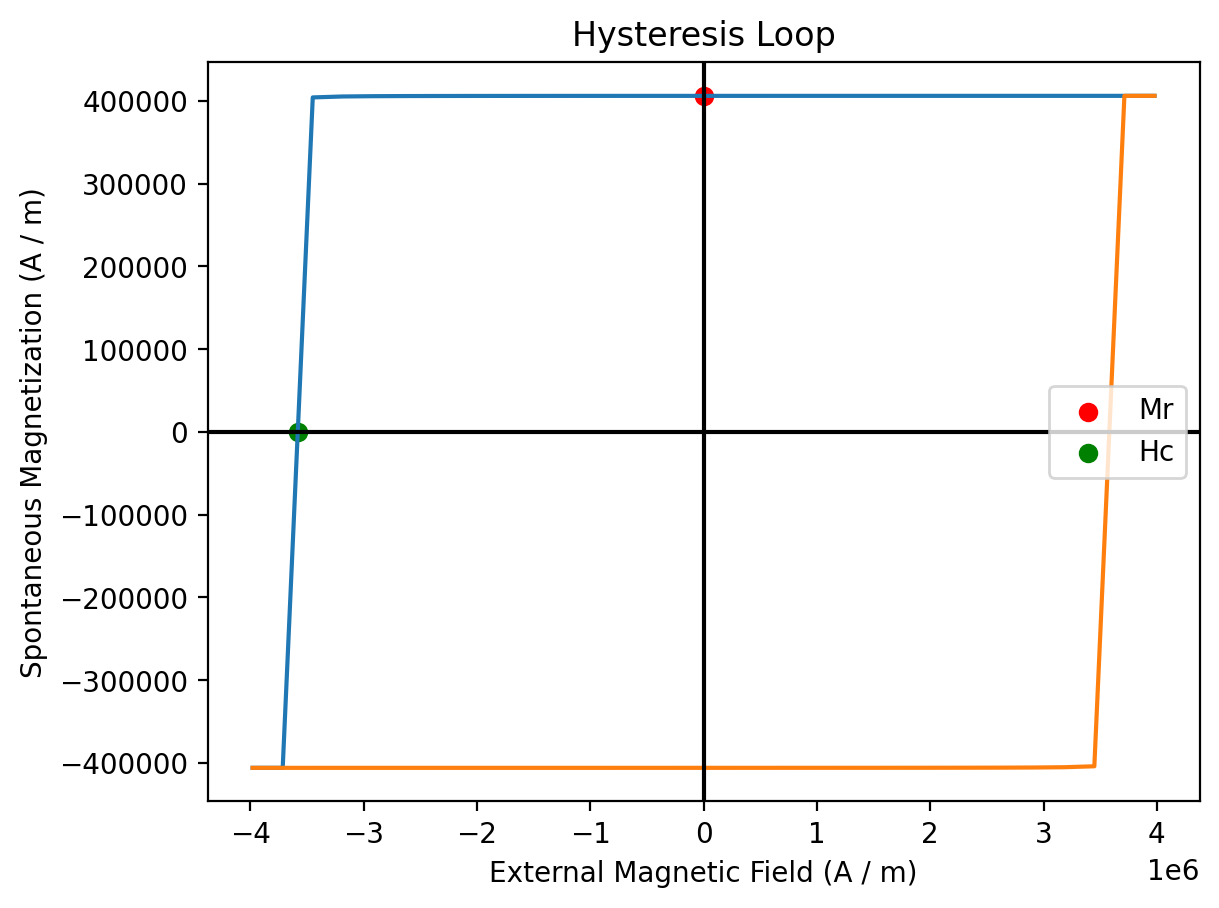
We can combine the results_hysteresis.plot method with some custom code to show Hc and Mr in the hysteresis plot:
ax = results_hysteresis.plot()
ax.scatter(0, extrinsic_properties.Mr.value, c="r", label="Mr")
ax.scatter(-extrinsic_properties.Hc.value, 0, c="g", label="Hc")
ax.axhline(0, c="k") # Horizontal line at M=0
ax.axvline(0, c="k") # Vertical line at H=0
ax.legend();
Compute Hc(T)#
We can leverage mammos to calculate Hc(T) for multiple values of T.
First, we run hysteresis simulations at 7 different temperatures and collect all simulation results:
T = np.linspace(0, 1.1 * results_kuzmin.Tc.q, 7)
simulations = []
for temperature in T:
print(f"Running simulation for T={temperature:.0f}")
results_hysteresis = mammos_mumag.hysteresis.run(
mesh="cube20_singlegrain_msize2",
Ms=results_kuzmin.Ms(temperature),
A=results_kuzmin.A(temperature),
K1=results_kuzmin.K1(temperature),
theta=0,
phi=0,
h_start=(9 * u.T).to(u.A / u.m),
h_final=(-9 * u.T).to(u.A / u.m),
h_n_steps=30,
)
simulations.append(results_hysteresis)
Running simulation for T=0 K
Running simulation for T=98 K
Running simulation for T=197 K
Running simulation for T=295 K
Running simulation for T=394 K
Running simulation for T=492 K
Running simulation for T=591 K
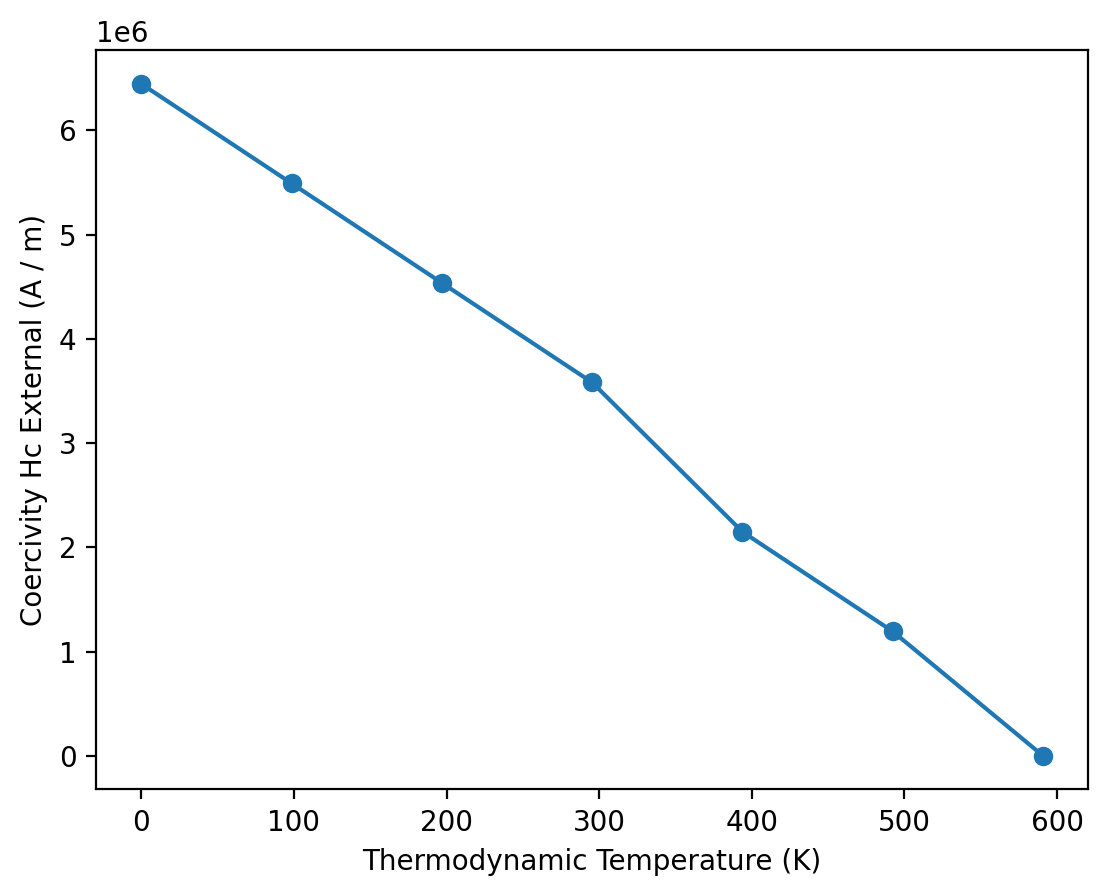
We can now use mammos_analysis.hysteresis as shown before to extract Hc for all simulations and visualize Hc(T):
Hcs = []
for res in simulations:
cf = mammos_analysis.hysteresis.extract_coercive_field(H=res.H, M=res.M).value
if np.isnan(cf): # Above Tc
cf = 0
Hcs.append(cf)
plt.plot(T, Hcs, linestyle="-", marker="o")
plt.xlabel(me.T().axis_label)
plt.ylabel(me.Hc().axis_label);
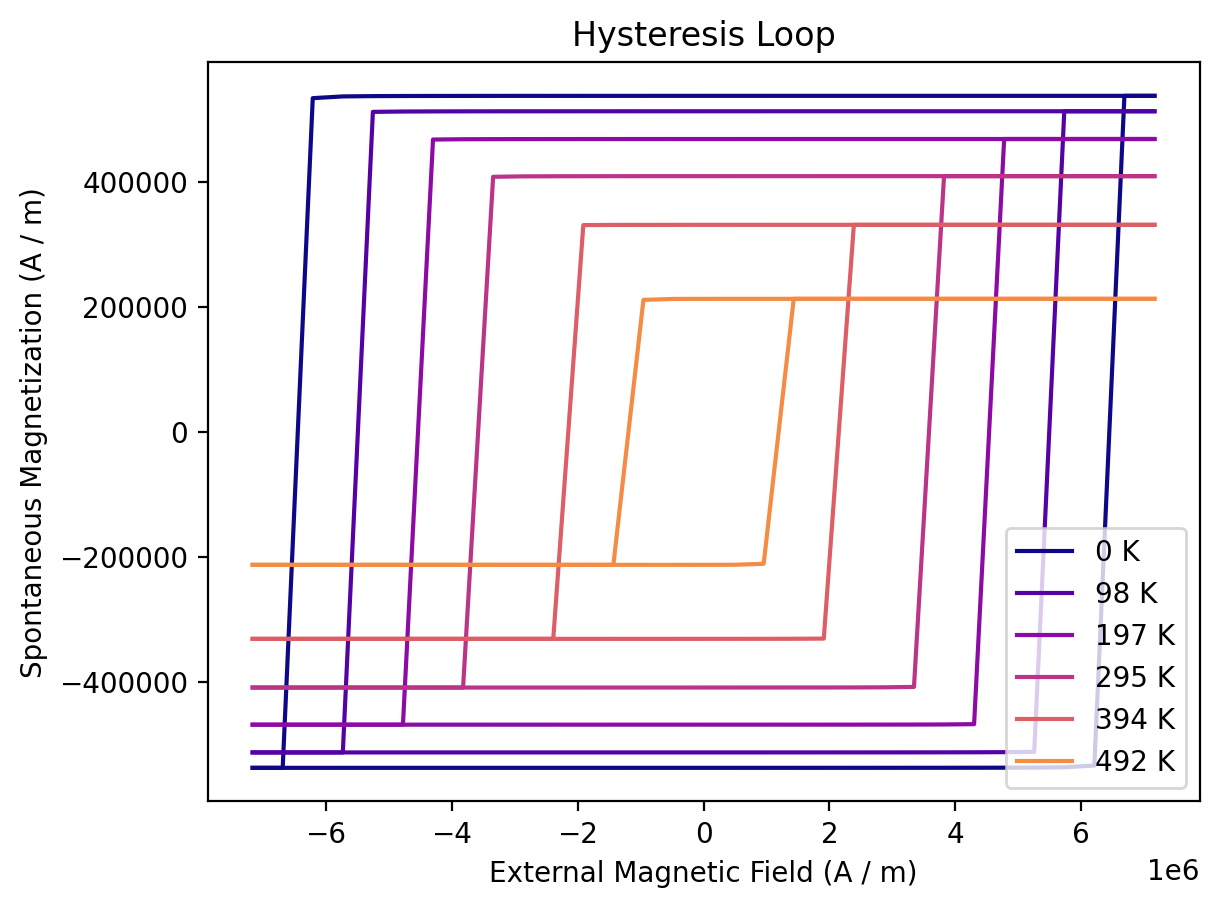
We can also show the hysteresis loops of all simulations:
colors = colormaps["plasma"].colors[:: math.ceil(256 / len(T))]
fix, ax = plt.subplots()
for temperature, sim, color in zip(T, simulations, colors, strict=False):
if np.isnan(sim.M.q).all(): # no Ms above Tc
continue
sim.plot(ax=ax, label=f"{temperature:.0f}", color=color, duplicate_change_color=False)
ax.legend(loc="lower right");
MODA for the workflow#
